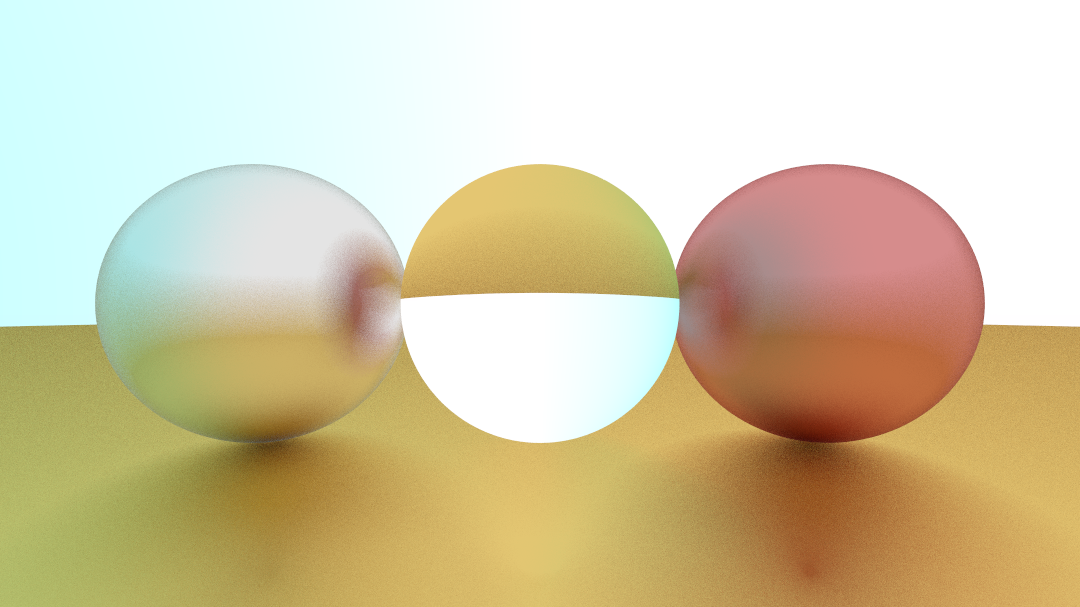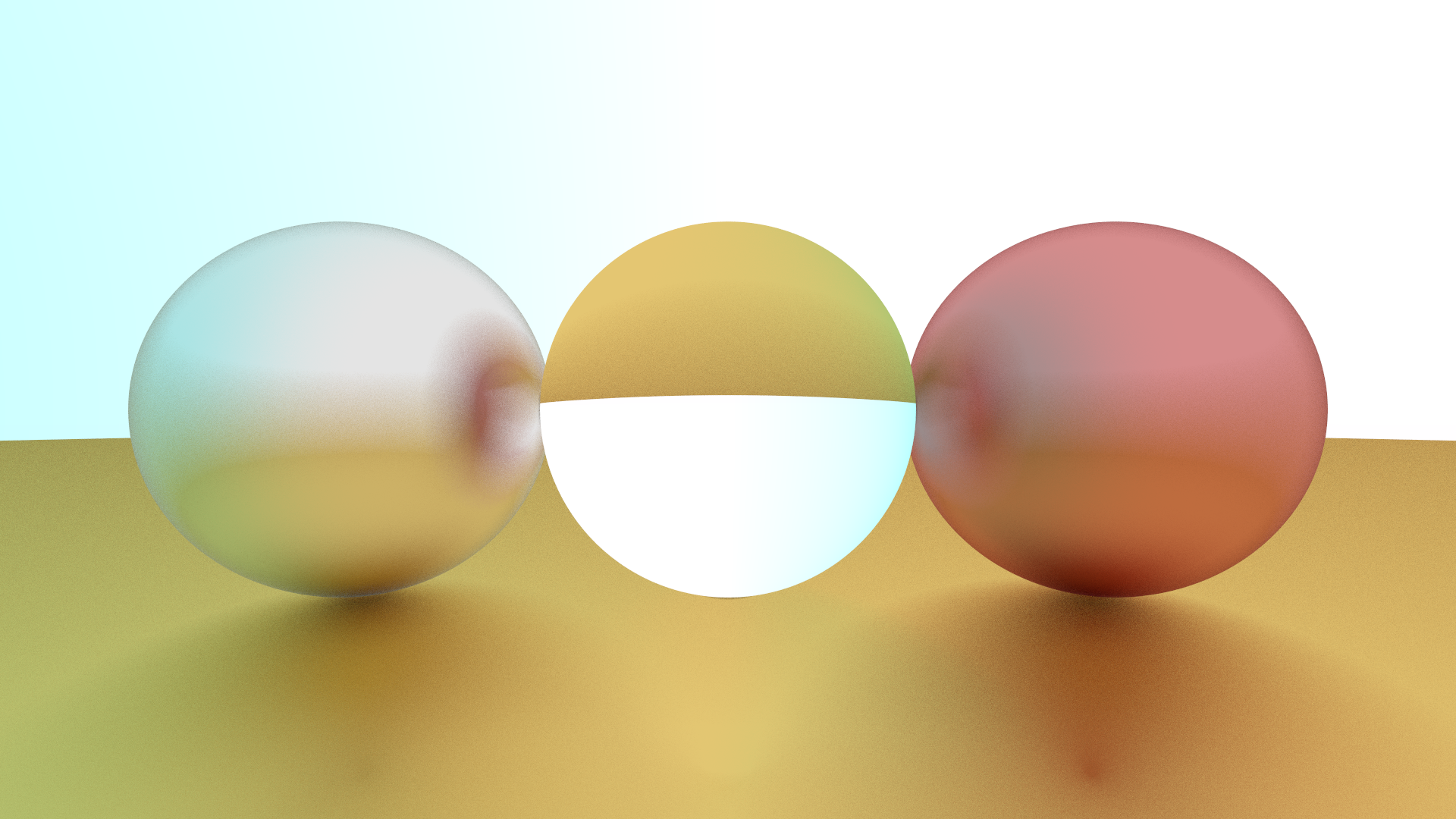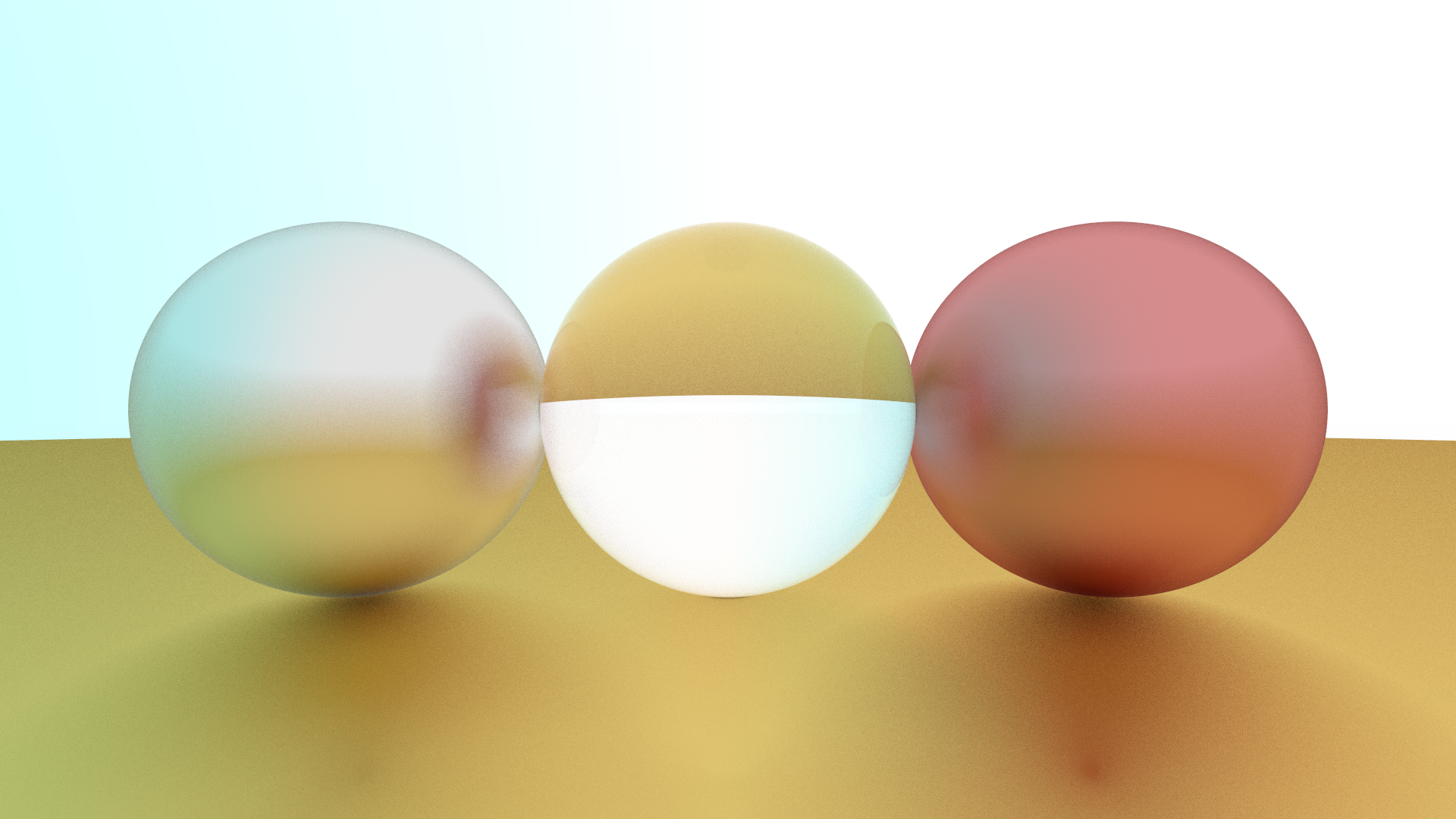Note on "Ray tracing in one week" - Part 6

Note on "Ray tracing in one week" - Part 6

Ayano Kagurazaka Lv3
  2024-02-05 2024-02-05 Created   2025-04-28 21:40:37 2025-04-28 21:40:37 Updated      2.3k Words  14 Mins  

# Note on “Ray tracing in one week” - Part 6

Dielectrics, rather than the definition in circuits, is material that reflects and refracts light. The most common example is glass. We have already implemented reflection, and now we are going to implement refraction.

# Snell’s law and refraction

When calculating refracted ray, we use Snell’s law. Snell’s law stated that: given two medium with refractive index η\eta and η′\eta', a ray with incidence angle \theta and refraction angle \theta' will satisfy the following equation:

ηsin⁡(θ)=η′sin⁡(θ′)\eta \sin(\theta) = \eta' \sin(\theta')

The diagram below shows the refraction of light from air to glass(assumed to have refractive index of 1.5). I\mathbf{I} is the incident ray, and R\mathbf{R} is the refracted ray. We can derive the vector formula of R with I and the normal vector n\mathbf{n} of the surface.

refraction

Since we only need the direction of the refracted ray, we can treat the incident ray and the normal vector as unit vectors. By simple trig, we have:

Ix=sin⁡(θ)⋅NRx=sin⁡(θ′)⋅N\begin{align*} \mathbf{I}_x &= \sin(\theta) \cdot\mathbf{N}\\ \mathbf{R}_x &= \sin(\theta') \cdot\mathbf{N}\\ \end{align*}

And by Snell’s law, we have:

ηsin⁡(θ)=η′sin⁡(θ′)sin⁡(θ′)=ηη′⋅sin⁡(θ)\begin{align*} \eta \sin(\theta) &= \eta' \sin(\theta') \\ \sin(\theta') &= \frac{\eta}{\eta'}\cdot \sin(\theta) \\ \end{align*}

Substitute, we have:

Rx=sin⁡(θ′)Rx=ηη′⋅sin⁡(θ)Rx=ηη′⋅Ix\begin{align*} \mathbf{R}_x &= \sin(\theta') \\ \mathbf{R}_x &= \frac{\eta}{\eta'}\cdot \sin(\theta) \\ \mathbf{R}_x &= \frac{\eta}{\eta'}\cdot \mathbf{I}_x \\ \end{align*}

By vector addition and geometry, we have:

Ix=I+ny=I+N⋅cos⁡θ\mathbf{I}_x = \mathbf{I} + \mathbf{n}_y = \mathbf{I} + \mathbf{N} \cdot \cos{\theta}

Substitute, we have:

Rx=ηη′⋅Ix=ηη′⋅(I+N⋅cos⁡θ)\begin{align*} \mathbf{R}_x &= \frac{\eta}{\eta'}\cdot \mathbf{I}_x \\ &= \frac{\eta}{\eta'}\cdot (\mathbf{I} + \mathbf{N} \cdot \cos{\theta}) \\ \end{align*}

And we can derive the Ry\mathbf{R_y} by using Pythagorean theorem:

Ry=−1−∣∣R∣∣x2⋅N\mathbf{R}_y = -\sqrt{1 - ||\mathbf{R}||_x^2}\cdot\mathbf{N}

This is good, but cos⁡\cos for θ\theta is not easy to calculate. We can use the following formula to calculate cos⁡θ\cos{\theta} if theta is the angle between two normalized vectors A\mathbf{A} and B\mathbf{B}:

cos⁡θ=A⋅B\cos{\theta} = \mathbf{A} \cdot \mathbf{B}

and Rx\mathbf{R}_x is:

Rx=ηη′⋅(I+N⋅cos⁡θ)=ηη′⋅(I+N⋅⟨I,N⟩)\begin{align*} \mathbf{R}_x &= \frac{\eta}{\eta'}\cdot (\mathbf{I} + \mathbf{N} \cdot \cos{\theta}) \\ &= \frac{\eta}{\eta'}\cdot (\mathbf{I} + \mathbf{N} \cdot \langle \mathbf{I} ,\mathbf{N}\rangle )\\ \end{align*}

We can implement this in code like this:

icon-padding

MathUtil.h

1
2
3
4
5
6
7
    class Vec3 {
//...

		static Vec3 refract(const Vec3 &uv, const Vec3 &n, double etai_over_etat);

//...
    };

icon-padding

MathUtil.cpp

1
2
3
4
5
6
Vec3 Vec3::refract(const Vec3 &uv, const Vec3 &n, double etai_over_etat) {
	auto cos_theta = fmin((-uv).dot(n), 1.0);
	Vec3 refr_x = etai_over_etat * (uv * cos_theta * n);
	Vec3 refr_y = -sqrt(fabs(1.0 - refr_x.lengthSq())) * n;
	return refr_x + refr_y;
}

and now we define our dielectric material:

icon-padding

Material.h

1
2
3
4
5
6
7
8
9
10
11
class Dielectric : public IMaterial {
public:
	Dielectric(double idx, const ImageUtil::Color &albedo);

	bool scatter(const MathUtil::Ray &r_in, const HitRecord &record, MathUtil::Vec3 &attenuation,
				 MathUtil::Ray &scattered) const override;

private:
	double ir;
	ImageUtil::Color albedo;
};

icon-padding

Material.cpp

1
2
3
4
5
6
7
8
9
bool Dielectric::scatter(const MathUtil::Ray &r_in, const HitRecord &record, MathUtil::Vec3 &attenuation,
						 MathUtil::Ray &scattered) const {
	attenuation = albedo;
	double ref_ratio = record.front_face ? (1.0 / ir) : ir;

	auto refracted = MathUtil::Vec3::refract(r_in.dir().unit(), record.normal, ref_ratio);
	scattered = MathUtil::Ray(record.p, refracted);
	return true;
}

We add some code to the main function to test the dielectric material:

icon-padding

main.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include "ImageUtil.h"
#include "GraphicObjects.h"
#include "Material.h"

int main() {
	auto camera = Camera(1920, 16.0 / 9.0, 2.0, 1, MathUtil::Point3(0, 0, 1));
	auto world = HittableList();
	auto center_ball_material = std::make_shared<Dielectric>(Dielectric(1.5, ImageUtil::Color(1.0, 1.0, 1.0)));
	auto right_ball_material = std::make_shared<Metal>(Metal(ImageUtil::Color(0.7, 0.3, 0.3), 0.4));
	auto left_ball_material = std::make_shared<Metal>(Metal(ImageUtil::Color(0.8, 0.8, 0.8), 0.4));
	auto ground_material = std::make_shared<Metal>(Metal(ImageUtil::Color(0.8, 0.6, 0.2), 0.4));
	world.add(std::make_shared<Sphere>(Sphere(1000, {0, -1000.5, -1.0}, ground_material)));
	world.add(std::make_shared<Sphere>(Sphere(0.5, {0, 0, -1}, center_ball_material)));
	world.add(std::make_shared<Sphere>(Sphere(0.5, {-1, 0, -1.0}, left_ball_material)));
	world.add(std::make_shared<Sphere>(Sphere(0.5, {1, 0, -1.0}, right_ball_material)));
	camera.setSampleCount(100);
	camera.setRenderDepth(50);
	camera.setRenderThreadCount(24);
	camera.Render(world, "out", "test.ppm");
	return 0;
}

The result is:

dielectric

# Full reflection

Consider the equation deduced from Snell’s law:

sin⁡θηη′=sin⁡θ′\sin{\theta} \frac{\eta}{\eta'} = \sin{\theta'}

When η>η′\eta > \eta', for some value of θ\theta, the right-hand side will be greater than 1, and there will be no real solution for θ′\theta'. This means that the light will be fully reflected.

Since sin⁡\sin takes too much time to calculate, we can use our old friend, the dot product, to calculate sin⁡θ\sin{\theta}:

cos⁡θ=I⋅Nsin⁡θ=1−cos⁡2θ=1−(I⋅N)2\begin{align*} \cos{\theta} &= \mathbf{I} \cdot \mathbf{N} \\ \sin{\theta} &= \sqrt{1 - \cos^2{\theta}} \\ &= \sqrt{1 - (\mathbf{I} \cdot \mathbf{N})^2} \\ \end{align*}

We can use this to calculate the reflectance of the dielectric material:

icon-padding

Material.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
bool Dielectric::scatter(const MathUtil::Ray &r_in, const HitRecord &record, MathUtil::Vec3 &attenuation,
						 MathUtil::Ray &scattered) const {
	attenuation = albedo;
	double ref_ratio = record.front_face ? (1.0 / ir) : ir;
	auto unit = r_in.dir().unit();

	double cos = fmin((-unit).dot(record.normal), 1.0);
	double sin = sqrt(1 - cos * cos);

	bool can_refr = ref_ratio * sin < 1.0;
	MathUtil::Vec3 dir;

	if(can_refr)
		dir = MathUtil::Vec3::refract(r_in.dir().unit(), record.normal, ref_ratio);
	else
		dir = MathUtil::Vec3::reflect(r_in.dir().unit(), record.normal);

	scattered = MathUtil::Ray(record.p, dir);
	return true;
}

The result:

fullRefl

# Schlick’s approximation

Normally, real glass becomes more reflective as the angle of incidence increases. This is called Fresnel effect. Schlick’s approximation is a simple way to approximate the reflectance of a dielectric material. The formula is:

R(θ)=R0+(1−R0)(1−cos⁡θ)5R(\theta) = R_0 + (1 - R_0)(1 - \cos{\theta})^5

where:

R0=(η−η′η+η′)2R_0 = (\frac{\eta - \eta'}{\eta + \eta'})^2

and θ\theta is the incident angle.

We can implement this in our code:

icon-padding

Material.h

1
2
3
4
5
6
7
8
9
10
11
12
class Dielectric : public IMaterial {
public:
	Dielectric(double idx, const ImageUtil::Color &albedo);

	bool scatter(const MathUtil::Ray &r_in, const HitRecord &record, MathUtil::Vec3 &attenuation,
				 MathUtil::Ray &scattered) const override;
private:
	double ir;
	ImageUtil::Color albedo;
	static double reflectance(double cosine, double refr_idx);
};

icon-padding

Material.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
bool Dielectric::scatter(const MathUtil::Ray &r_in, const HitRecord &record, MathUtil::Vec3 &attenuation,
						 MathUtil::Ray &scattered) const {
	attenuation = albedo;
	double ref_ratio = record.front_face ? (1.0 / ir) : ir;
	auto unit = r_in.dir().unit();

	double cos = fmin((-unit).dot(record.normal), 1.0);
	double sin = sqrt(1 - cos * cos);

	bool can_refr = ref_ratio * sin < 1.0;
	MathUtil::Vec3 dir;

	if(can_refr && reflectance(cos, ref_ratio) < MathUtil::randomDouble())
		dir = MathUtil::Vec3::refract(r_in.dir().unit(), record.normal, ref_ratio);
	else
		dir = MathUtil::Vec3::reflect(r_in.dir().unit(), record.normal);

	scattered = MathUtil::Ray(record.p, dir);
	return true;
}
double Dielectric::reflectance(double cosine, double refr_idx) {
	auto r0 = (1 - refr_idx) / (1 + refr_idx);
	r0 *= r0;
	return r0 + (1 - r0) * std::pow(1 - cosine, 5);
}

The result:

schlick

icon-padding

Notice the edge of the glass sphere. The reflection is stronger than the center and you can see the reflection of the other spheres.

# Zooming in

Right now we have the ability to position our camera, but not yet to rotate or change the zoom. Let’s implement the second feature first, and it can be implemented by adjusting the field of view.

Field of view is the max angle of the ray that the camera can see. Give a FOV and the aspect ratio, we can calculate the height and width of the viewport. The formula is:

Vheight=2⋅tan⁡(θ2)Vwidth=Vheight⋅R\begin{align*} V_{height} &= 2 \cdot \tan(\frac{\theta}{2})\\ V_{width} &= V_{height} \cdot R \end{align*}

Where VV is the viewport, θ\theta is the field of view, and RR is the aspect ratio.

If we view the yz plane from x direction, the fov will be like this:

fov

We can implement this in our camera class:

icon-padding

GraphicObjects.h

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
class Camera {
public:
    Camera(int width, double aspect_ratio, double fov, double focal_len, MathUtil::Point3 position);

    int getWidth() const;

    int getHeight() const;

    double getAspectRatio() const;

    double getViewportWidth() const;

    double getViewportHeight() const;

    double getFocalLen() const;

	int getSampleCount() const;

	double getFov() const;

    const MathUtil::Point3 &getPosition() const;

    const MathUtil::Vec3 &getHoriVec() const;

    const MathUtil::Vec3 &getVertVec() const;

    const MathUtil::Vec3 &getPixDeltaX() const;

    const MathUtil::Vec3 &getPixDeltaY() const;

    const MathUtil::Point3 &getViewportUl() const;

    const MathUtil::Point3 &getPixel00() const;

    void setWidth(int width);

    void setAspectRatio(double aspect_ratio);

    void setFocalLen(double focal_len);

    void setPosition(const MathUtil::Point3 &position);

	void setSampleCount(int sample_count);

	void setFov(double fov);

    [[nodiscard]] MathUtil::Vec3 getPixelVec(int x, int y) const;

    [[nodiscard]] MathUtil::Vec3 getPixRayDir(int x, int y) const;

	void Render(const IHittable& world, const std::string& path, const std::string& name);

	int getRenderDepth() const;

	void setRenderDepth(int renderDepth);

	int getRenderThreadCount() const;

	void setRenderThreadCount(int renderThreadCount);

private:

	std::vector<std::vector<ImageUtil::Color>> RenderWorker(const IHittable &world, int start, int end);

	ImageUtil::Color rayColor(const MathUtil::Ray &ray, const IHittable &object, int depth);

    void updateVectors();

	MathUtil::Vec3 randomDisplacement() const;

    int width;
    int height;
    double aspect_ratio;
    double viewport_width;
    double viewport_height;
    double focal_len;
	double fov = 45;
	int sample_count = 20;
	int render_depth = 50;
	int render_thread_count = 0;
    MathUtil::Point3 position;
    MathUtil::Vec3 hori_vec;
    MathUtil::Vec3 vert_vec;
    MathUtil::Vec3 pix_delta_x;
    MathUtil::Vec3 pix_delta_y;
    MathUtil::Point3 viewport_ul;
    MathUtil::Point3 pixel_00;
};

icon-padding

GraphicObjects.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
Camera::Camera(int width, double aspect_ratio, double fov, double focal_len,
               MathUtil::Point3 position) : width(width), aspect_ratio(aspect_ratio),
                                                   fov(fov), focal_len(focal_len),
                                                   position(std::move(position)),
                                                   height(static_cast<int>(width / aspect_ratio)),viewport_height(viewport_width / (static_cast<double>(width) / static_cast<double>(height))) {
    updateVectors();

}

void Camera::updateVectors() {
	auto theta = deg2Rad(fov);
	auto h = tan(theta / 2);
	viewport_height = 2 * h * focal_len;
	viewport_width = viewport_height * (static_cast<double>(width) / height);
    hori_vec = MathUtil::Vec3(viewport_width, 0, 0);
    vert_vec = MathUtil::Vec3(0, -viewport_height, 0);
    pix_delta_x = hori_vec / width;
    pix_delta_y = vert_vec / height;
    viewport_ul = position - MathUtil::Vec3(0, 0, focal_len) - (vert_vec + hori_vec) / 2;
    pixel_00 = viewport_ul + (pix_delta_y + pix_delta_x) * 0.5;
}

//...

void Camera::setAspectRatio(double aspect_ratio) {
    Camera::aspect_ratio = aspect_ratio;
    height = static_cast<int>(width / aspect_ratio);
    updateVectors();
}

//...

void Camera::setFov(double fov) {
	this->fov = fov;
}
double Camera::getFov() const {
	return fov;
}

Now we modify our main function to see the result:

icon-padding

main.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include "ImageUtil.h"
#include "GraphicObjects.h"
#include "Material.h"

int main() {
	auto camera = Camera(1920, 16.0 / 9.0, 45, 1, MathUtil::Point3(0, 0, 1));
	auto world = HittableList();
	auto center_ball_material = std::make_shared<Metal>(Metal(ImageUtil::Color(0.8, 0.8, 0.8), 0.4));
	auto ground_material = std::make_shared<Metal>(Metal(ImageUtil::Color(0.8, 0.6, 0.2), 0.4));
	world.add(std::make_shared<Sphere>(Sphere(1000, {0, -1000.5, -1.0}, ground_material)));
	world.add(std::make_shared<Sphere>(Sphere(0.5, {0, 0, -1}, center_ball_material)));
	camera.setSampleCount(100);
	camera.setRenderDepth(50);
	camera.setRenderThreadCount(24);
	camera.Render(world, "out", "test.ppm");
	return 0;
}

The result:

FOV = 90:

fov90

FOV = 45:

fov45

Recommended reading~
Note on Note on "Ray tracing in one week" - Part 7 Note on Note on "Ray tracing in one week" - Part 0 Note on Note on "Ray tracing in one week" - Part 5
Recommended reading~
Note on Note on "Ray tracing in one week" - Part 7 Note on Note on "Ray tracing in one week" - Part 0
Comments
On this page
Note on "Ray tracing in one week" - Part 6
  1. Note on “Ray tracing in one week” - Part 6
    1. Snell’s law and refraction
      1. Full reflection
      2. Schlick’s approximation
    2. Zooming in